Question

Solve the given differential equation by undetermined coefficients.

y''' − 3y'' + 3y' − y = ex − x + 21

Answer 1

Y =
`e^(t)` +
`te^(t)` +
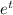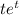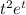`t^(2) e^(t)` + t - 18

Explanation:

y''' − 3y'' + 3y' − y = ex − x + 21

Homogeneous solution:

First we propose a solution:

Yh =
`e^(r*t)`

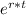
Y'h =
`r*e^(r*t)`

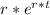
Y''h =
`r^(2)*e^(r*t)`

Y'''h =
`r^(3)*e^(r*t)`

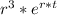
Now we solve the following equation:

Y'''h - 3*Y''h + 3*Y'h - Yh = 0

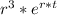`r^(3)*e^(r*t)` - 3*
`r^(2)*e^(r*t)` + 3*
`r*e^(r*t)` -
`e^(r*t)` = 0

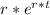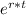`r^(3) - 3r^(2) + 3r - 1 = 0`

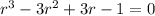
To solve the equation we must propose a solution to the polynomial :

r = 1

To find the other r we divide the polynomial by (r-1) as you can see

attached:

solving the equation:

(r-1)(
`r^(2) - 2r + 1`) = 0

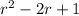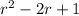`r^(2) - 2r + 1` = 0

r = 1

So we have 3 solution
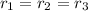`r_(1) = r_(2) =r_(3)` = 1

replacing in the main solution

Yh =
`e^(t)` +
`te^(t)` +
`t^(2) e^(t)`

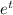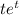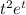
The t and
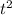`t^(2)` is used because we must have 3 solution linearly independent

Particular solution:

We must propose a Yp solution:

Yp =
`c_(1) (t^(3) + t^(2) + t + c_(4) )e^(t) + c_(2) t + c_(3)`

Y'p =
`c_(1)(t^(3) + t^(2) + t + c_(4) )e^(t) + c_(1)( 3t^(2) + 2t + 1 )e^(t) + c_(2)`

Y''p =
`c_(1)(t^(3) + t^(2) + t + c_(4) )e^(t) + c_(1)(6t + 2)e^(t)`

Y'''p =
`c_(1)(t^(3) + t^(2) + t + c_(4) )e^(t) + 6c_(1)e^(t)`

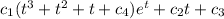
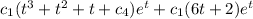
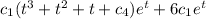
Y'''p - 3*Y''p + 3*Y'p - Yp =
`e^(t) - t + 21`

`6c_(1)e^(t) - 18c_(1) te^(t) - 6c_(1) e^(t) + 6c_(1) te^(t) + 9c_(1) t^(2) e^(t) + 3c_(1)e^(t) + 3c_(2) - c_(2) t -  c_(3)` =
`e^(t) - t + 21`

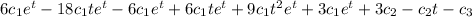equalizing coefficients of the same function:

- 12c_{1} = 0

9c_{1} = 0

3c_{1} = 0

c_{1} = 0

3c_{2} - c_{3} = 21 => c_{5} =
`(1)/(3)`

-c_{2} = -1

c_{2} = 1

c_{3} = -18

Then we have:

Y =
`e^(t)` +
`te^(t)` +
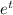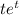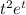`t^(2) e^(t)` + t - 18