Question

When the outliers are removed how does the mean change?

1 dot on 50
2 dots on 72
1 dot on 74
1 dot on 76
1 dot on 78
3 dots in between 78 and 80
1 dot on 80
1 dot between 80 and 82
3 dots on 82
the mean decreases by 1.9
the mean decreases by 2.4
the mean decreases by 1.9
there are no outliers
​

Answer 1

2.4

Step-by-step

Answer 2

Answer: The mean increases by 2.1

Explanation:

According to the given description (dots are denoting the frequency for each value), the given data is :-

50 , 72, 72 , 74, 76 , 78 , 79 , 79 , 79 80, 81, 82, 82, 82

[Note - We take 79 as the value between 78 and 80, 81 as between 80 and 82 ]

Mean =
`\overline{x}_1=\frac{\text{Sum of observations}}{\text{No. of observations}}` (1)

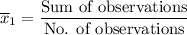`=(1066)/(14)=76.1428571429\approx76.1`

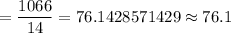
First Quartile:
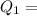`Q_1=` Median of the lower half ( 50 , 72, 72 , 74, 76 , 78 , 79 )

= 74

Third Quartile:
`Q_3=` Median of the upper half ( 79 , 79 80, 81, 82, 82, 82 )

= 81

Interquartile range (IQR)=
`Q_3-Q_1=81-74=7`

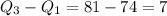
According to the IQR rule,

Upper limit =
`1.5* IQR+Q_3=1.5*7+81=91.5`

Lower limit =
`Q_1-1.5* IQR=74-1.5*7=63.5`

Since 50 < 63.2 , so 50 is outlier .

When 50 is removed from the data , the new data will be 72, 72 , 74, 76 , 78 , 79 , 79 , 79 80, 81, 82, 82, 82

Mean =
`\overline{x}_2=\frac{\text{Sum of observations}}{\text{No. of observations}}`

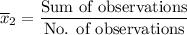
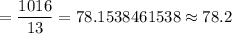`=(1016)/(13)=78.1538461538\approx78.2` (2)

Change in mean from (1) and (2)

`\overline{x}_2-\overline{x}_1\\\\=78.2-76.1=2.1`

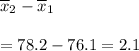
Hence, the mean increases by 2.1.