Question

Use differentiation rules to find the values of a and b that make the function f(x) = ( x 2 if x ≤ 2, ax3 + bx if x > 2 differentiable at x = 2.

Answer 1

The values of a and b are
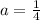`a=(1)/(4)` and b = 1

Explanation:

* Lets explain how to solve the equation

f(x) = {x² x ≤ 2

{ax³ + bx x > 2

* We need to find the values of a , b that make the function

differentiable at x = 2

- At first for f(x) to be continuous at x = 2, substitute x by two in the

the two expressions and equate them

∵ f(x) = x² at x ≤ 2 and f(x) = ax³ + bx at x > 2

∴ f(2) = (2)² = 4 ⇒ (1)

∴ f(2) = a(2)³ + b(2)

∴ f(2) = 8a + 2b ⇒ (2)

- Equate (1) and (2)

∴ 8a + 2b = 4 ⇒ (3)

* For f(x) to be differentiable when x = 2, the function must be

continuous when x = 2 and the one-sided derivatives must be

equal when x = 2

# Remember: If
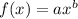`f(x)=ax^(b)` , then
`f'(x)=abx^(b-1)`

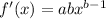
If
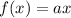`f(x)=ax` , then
`f'(x)=a`

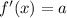
If
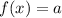`f(x)=a` , then
`f'(x)=0`

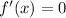
∵ f(x) = x²

∴ f'(x) = 2x

- Substitute x by 2

∴ f'(2) = 2(2) = 4

∴ f'(2) = 4 ⇒ (4)

∵ f(x) = ax³ + bx

∴ f'(x) = 3ax² + b

- substitute x by 2

∴ f'(2) = 3a(2)² + b

∴ f'(2) = 12a + b ⇒ (5)

- Equate (4) and (5)

∴ 12a + b = 4 ⇒ (6)

* Now we have system of equations

8a + 2b = 4 ⇒ (3)

12a + b = 4 ⇒ (6)

- Multiply equation (6) by -2 to eliminate b

∴ -24 a - 2b = -8 ⇒ (7)

- Add equations (3) and (7)

∴ -16a = -4

- Divide both sides by -16

∴ a =
`(1)/(4)`

- substitute the value of a in equation (6)

∴
`12((1)/(4))+b=4`

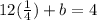
∴ 3 + b = 4

- Subtract 3 from both sides

∴ b = 1

* The values of a and b are
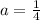`a=(1)/(4)` and b = 1