Question

Reaction Rates

Part A

For the arbitrary reaction,

A + B ? C + D

The following initial rates were measured given the initial concentrations of A and B. Determine the rate order for both A and B.

[A]o [B]o Initial Rate (M/s)
0.12 0.22 0.00639
0.24 0.22 0.0128
0.12 0.11 0.00639

Part B

-0th order in A and 1st order in B
-2nd order in A and 0th order in B
-1st order in A and 1st order in B
-1st order in A and 0th order in B
The following arbitrary reaction is exothermic:

A + B ? C + D

Predict what will happen to the rate of the reaction if the temperature is increased.

-The reaction rate will decrease.
-Equilibrium is shifted to the left.
-The reaction rate increases.
-There will be no change in rate.

Answer 1

PART A 1st order in A and 0th order in B

Part B The reaction rate increases

Step-by-step explanation:

PART A

The rate law of the arbitrary chemical reaction is given by

`-r_A=k*\left[A\right]^\alpha*\left[B\right]^\beta\bigm`

Replacing for the data

Expression 1
`0.00639=k*{0.12}^\alpha*{0.22}^\beta`

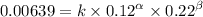
Expression 2
`0.01280=k*{0.24}^\alpha*{0.22}^\beta`

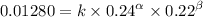
Expression 3
`0.00639=k*{0.12}^\alpha*{0.11}^\beta`

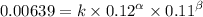
Making the quotient between the fist two expressions

`(0.00639)/(0.01280)=\left((0.12)/(0.24)\right)^\alpha`

Then the expression for
`\alpha`

`\alpha=(ln(0.00639)/(0.01280))/(ln(0.12)/(0.24))=1\bigm`

Doing the same between the expressions 1 and 3

`(0.00639)/(0.00639)=\left((0.22)/(0.11)\right)^\beta`

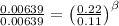
Then

`\beta=(ln(0.00639)/(0.00639))/(ln(0.22)/(0.11))=0\bigm`

This means that the reaction is 1st order respect to A and 0th order respect to B .

PART B

By the molecular kinetics theory, if an increment in the temperature occurs, the molecules will have greater kinetic energy and, consequently, will move faster. Thus, the possibility of colliding with another molecule increases. These collisions are necessary for the reaction. Therefore, an increase in temperature necessarily produces an increase in the reaction rate.