Answer:
D(-1,0)
Explanation:
Plot points A(-3, 2), B(-1, 4), and C(1, 2) on the coordinate plane (see attached diagram).
Two sides AB and BC are of equal length and are perpendicular, because
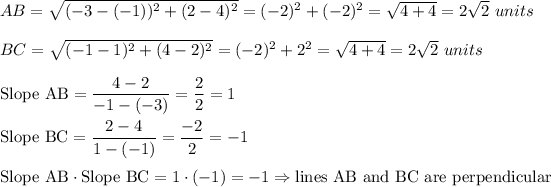
If the quadrilateral ABCD has all sides perpendicular, then ABCD is a square. The diagonals of the square bisects each other. Find the coordinates of the point of intersection of these diagonals. This is the midpoint of segment AC:
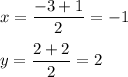
If point O(-1,2) is the point of intersection of diagonals, then it is the midpoint of the diagonal BD. Find coordinates of point D:
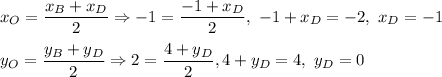
Thus, D(-1,0)