Question

vector L is 303m long in a 205 direction. Vector M is 555m long in a 105 direction. Find the magnitude and direction of the vector.

Answer 1

584.3 m at
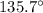`135.7^(\circ)` above the positive x-axis

Step-by-step explanation:

We have to find the magnitude and direction of the resultant vector. In order to do that, we have to resolve each vector along the x- and y- direction first.

Resolving the vector L:

`L_x = L cos \theta_L = 303 \cdot cos 205^(\circ) =-274.6m\\L_y = L sin \theta_L = 303 \cdot sin 205^(\circ) = -128.1 m`

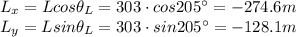
Resolving the vector M:

`M_x = M cos \theta_M = 555 \cdot cos 105^(\circ) =-143.6 m\\M_y = M sin \theta_M = 555 \cdot sin 105^(\circ) = 536.1 m`

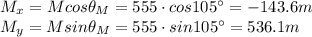
Now we can find the components of the resultant vector by adding the components of each vector along each direction:

`R_x = L_x + M_x = -274.6 +(-143.6)=-418.2 m\\R_y = L_y + M_y = -128.1 +536.1 = 408 m`

So the magnitude of the resultant vector is

`R=√(R_x^2 + R_y^2)=√((-418.2)^2+(408)^2)=584.3 m`

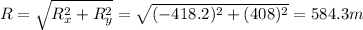
While the direction is given by:

`\theta = tan^(-1) (R_y)/(R_x)=tan^(-1) (408)/(418.2)=44.3^(\circ)`

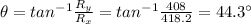
But since
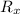`R_x` is negative and
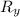`R_y` is positive, it means that this angle is measured as angle above the negative x-axis; so the direction of the vector is actually

`\theta = 180^(\circ) - 44.3^(\circ) = 135.7^(\circ)`