Question

A charge of -6.50 nC is spread unifonnly over the surface of one face of a nonconducting disk of radius 1.25 cm. (a) Find the

magnitude and direction of the electric field this disk produces at a point P on the axis of the disk a distance of 2.00 cm from its center. (b) Suppose that the charge were all pushed away from the center and distributed unifonnly on the outer rim of the disk. Find the magnitude and direction of the electric field at point P. (c) If the charge is all brought tn the center of the disk, find the magnitude and direction of the electric field at point P. (d) Why is the field in part (a) stronger than the field in part (b)? Why is the field in part (c) the strongest of the three fields?

Answer 1

(a) Magnitude =
`1.14* 10^5\ N/C`

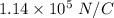
Direction = toward the center of the disc

(b) Magnitude =
`8.90* 10^4\ N/C`

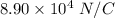
Direction = toward the center of the disc

(c) Magnitude =
`1.46* 10^5\ N/C`

Direction = toward the center of the disc

(d) See explanation

(e) See explanation.

Step-by-step explanation:

Given:

• k = Boltzmann constant =
  `9* 10^9\ Nm^2/C^2`

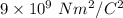
• Q = Uniformly spread charge on the disc =
  `-6.50\ \\C = -6.50* 10^(-9)\ C`

• x = distance of the point P from the center of disc on its axis = 2 cm = 0.02 m

• r = radius of the disc = 1.25 cm = 0.0125 m

Assume:

• E = electric field at point P on the axis

Part(a):

Using the formula for the electric field due to the uniform charged disc at a point P on its axis, we have

`E = (2 kQ)/(r^2)\left ( 1-(x)/(√(x^2+r^2)) \right )\\\Rightarrow E = (2 * 9* 10^9* (-6.50* 10^(-9)))/((0.0125)^2)\left ( 1-(0.02)/(√((0.02)^2+(0.0125)^2)) \right )\\\Rightarrow E =-1.14* 10^5\ N/C\\`

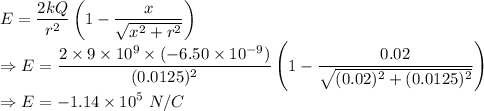
Hence, the magnitude of electric field at the given distance from the disc along its axis is
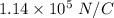`1.14* 10^5\ N/C` in the direction toward the center of the disc along the axis.

Part(b):

When all the charges on the disc are pushed away from the center of the disc to get uniformly distributed to its outer rim, the disc behaves like a uniformly charged ring.

Using the formula for the electric field due to the uniform charged ring at a point P on its axis, we have

`E= (kQx )/(\left ( √(x^2+r^2) \right )^3)\\\Rightarrow E = ( 9* 10^9* (-6.50* 10^(-9))* 0.02)/(\left ( √((0.02)^2+(0.0125)^2) \right )^3)\\&=-8.90* 10^4\ N/C`

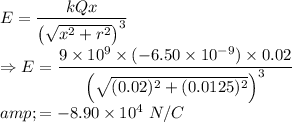
Hence, the magnitude of electric field at the given point from the rim along its axis is
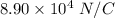`8.90* 10^4\ N/C`, and it is also toward the center of the along the axis.

Part (c):

When all the charge on the disc is pushed to the center of the disc, then the disc behaves as a point charge.

Using the formula of electric field due to a point charge at a fixed point, we have

`E = (kQ)/(x^2)\\\Rightarrow E = (9* 10^9* (-6.50* 10^(-9)))/((0.02)^2)\\\Rightarrow E = -1.46* 10^5`

Hence, the magnitude of electric field due to the point charge at the point P on the axis is
`1.46* 10^5\ N/C`. which also points toward the center of the disc along the axis.

The direction of the electric field is found toward the negative x-axis because the electric field due to a point negative charge is radially inward.

Part (d):

The magnitude of electric field in part (a) is stronger than that in part (b) because the disc in part (a) is composed of infinite number of rings having radius varying from 0 cm to 2.5 cm whose components along the axis of electric field are added together which is greater than the electric field produced by a single ring in part (b).

Hence, the electric field in part (a) is greater than the electric field in part (b).

Part (e):

The electric field in part (c) is the strongest of the three fields. This is because the field due to a point charge on the axis has the only component along the axis. However, the field components in part (a) and part (b) are distributed along two axes whose axial component is considerable and the other component gets canceled out. This causes the field strength to be weaker in part (a) and part (c).