Answer:
Given the equation of the particle, we know that:
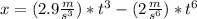
a) In
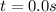 we evaluate
we evaluate
 in the former equation:
in the former equation:
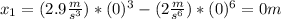
In
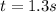
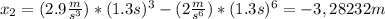
a) So, we know that the displacement of te particle is given by:
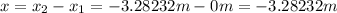
To find it's velocity, we need to derivate the equation of position by the formula:
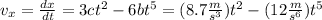
And evaluate this expression at each specified t:
b)

c)
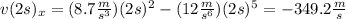
d)
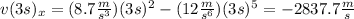
e)
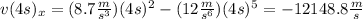
To find it's acceleration, we need to derivate the equation of velocity by the formula:
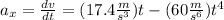
And evaluate this expression at each specified t:
f)
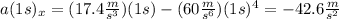
g)
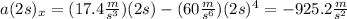
h)
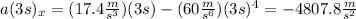
i)
