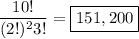BOOKKEEPER has 10 letters, so there are 10! total permutations if we treat each letter as distinct. In other words, BOOKKEEPER and BOOKKEEPER are the different words because the underlined K is treated as different from the non-underlined K.
But we want to treat these letters as the same. In any given permutation of BOOKKEEPER, there are 2! ways each of rearranging the Os and Ks, and 3! ways of rearranging the Es. So the total number of permutations is