Question

Ik it’s a lot i’m giving 50 for this and 50 for other one u may need to do other first to understand

Answer 1

Question 5. 4096.

Question 6. 1/4096.

Question 7. 350.

Question 8.
`6.7441*10^9`.

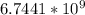Question 9.
`1.4828*10^(-10)`.

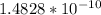Explanation:

Question 5.

If there are 6 questions, each of them with 4 possible answers, then the different possible key answers is given by multiplying 4, 6 times:

`4^6=4096.`

Question 6.

The probability of getting 1 correct answer is given by the amount of correct answers (we assume it's 1) divided by the total amount of answers on each question (4). Hence, probability of choosing the correct answer once is:

`(1)/(4)`.

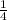Now, to find the probability of getting all 6 questions correct, we'll have to multiply the probability of getting 1 question right 6 times:

`(1)/(4) *(1)/(4) *(1)/(4) *(1)/(4) *(1)/(4) *(1)/(4) =((1)/(4)) ^6=(1)/(4096)`.

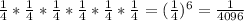Question 7.

In this question, apply the same logic as in Question 5, multiply all the choises to get the number of possible combinations:

`5*10*7=350`.

Question 8.

For this question, use the probability formula of permutations for different elements (no replacement).

Formula:
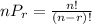`nP_r=(n!)/((n-r)!)`, where n is the number of different elements that can be drawn and r if the amount of selected elements. Substitute in the formula like this:

`nP_r=(46!)/((46-6)!)=(46!)/((40)!)=6.7441*10^9`.

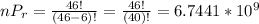Question 9.

The probabilty of getting the first number right is 1/46, for the second number is 1/45, because we already guessed the first number, the probability of guessing the third one is 1/44, and so on. Hence, the probability of getting a winner ticket is:

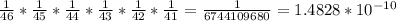`(1)/(46) *(1)/(45) *(1)/(44) *(1)/(43) *(1)/(42) *(1)/(41) =(1)/(6744109680) =1.4828*10^(-10)`.