Question

Answer for 1A. With explanation

Answer 1

Answer: x = 3, y = -1 → (3, -1)

Explanation:

When solving a system, you want the coefficients of one of the variables to be opposites (same number but different signs).

Multiply each equation by a number that will create one of the coefficients to be opposites. Then add the two equations to eliminate one of the variables.

2x - 5y = 11 → 3(2x - 5y = 11 ) → 6x - 15y = 33

-3x + 4y = -13 → 2(-3x + 4y = -13) → -6x + 8y = -26

-7y = 7

÷-7 ÷-7

y = -1

Now input y = -1 into either of the equations to solve for x

2x - 5y = 11

2x - 5(-1) = 11

2x + 5 = 11

2x = 6

x = 3

So, the solution to the system is: x = 3, y = -1 → (3, -1)

Using the table method, input values for x into each of the equations to solve for y. If both equations result in the same y-value, then that is your solution.

Try x = 0:

1st equation 2nd equation

2x - 5y₁ = 11 -3x + 4y₂ = -13

2(0) - 5y₁ = 11 -3(0) + 4y₂ = -13

0 - 5y₁ = 11 0 + 4y₂ = -13

y₁ =
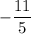`-(11)/(5)` y₂ =
`-(13)/(4)`

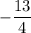
y₁ ≠ y₂ so this is not a solution

Do the same for x = 1, x = 2, and x = 3. The result is the table below.

`\begin{array}cx&y_1&y_2&(x,y_1)&(x,y_2)\\0&-(11)/(5)&-(13)/(4)&(0,-(11)/(5))&(0,-(13)/(4))\\\\1&-(9)/(5)&-(5)/(2)&(0,-(9)/(5))&(0,-(5)/(2))\\\\2&-(7)/(5)&-(7)/(4)&(0,-(7)/(5))&(0,-(7)/(4))\\\\3&-1&-1&(3,-1_&(3,-1)\end{array}\right]`