Question

A large rock of mass me materializes stationary at the orbit of Mercury and falls into the sun. Itf the Sun has a mass ms and radius rs and Mercury has an orbit of radius R, determine the speed which the rock hits the surface of the sun.

Answer 1

The answer is
`v = \sqrt{2G(M_s)/(R^2)(R-r_s)}`.

Step-by-step explanation:

From the law of gravity,

`F = G (Mm)/(r^2)`

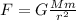
considering F as a conservative force,
`F = - \\abla U`,

the general expression for gravitational potential energy is

`U = -G (Mm)/(r)`,

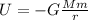where G is the gravitational constant, M and m are the mass of the attracting bodies, and r is the distance between their centers. The negative sign is because the force approaches zero for large distances, and we choose the zero of gravitational potential energy at an infinite distance away.

However, as the mass of the Sun is much greater than the mass of the rock, the gravitational acceleration is defined as

`g = -G (M)/(r^2)`,

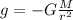(the negative sign indicates that the force is an attractive force), and the potential energy between the rock and the Sun is

`U = g M_e R`,

which is actually the total energy of the system, because the rock materializes stationary at this point (there is no radial kinetic energy).

When the rock hits the surface of the Sun, almost all potential energy is converted to kinetic energy, but not all because the Sun is not a puntual mass. So the potential energy converted to kinetic energy is

`U_p = g M_e(R- r_s)`,

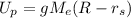then, the kinetik energy when the rock hits the surface is

`U_k =(1)/(2)M_e v^2 = g M_e(R- r_s)`,

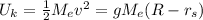so

`v = √(2g(R-r_s))`

where g is the gravitational acceleration generated by the Sun at R,

`g = G (M_s)/(R^2)`.