Question

The intensity level in decibels is defined as 10 log10(I/I0), where I0 is a reference intensity equal to the human threshold of hearing, 10–12 W/m2. What is the intensity of the threshold of pain, 120 decibels?

Answer 1

The intensity of the threshold of pain is 1 W/m²

Step-by-step explanation:

Given that,

Decibels = 120

`I_(0)=10^(-12)\ W/m^2`

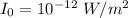
The intensity level in decibels is defined as

`dB=10 log_(10)((I)/(I_(0)))`

Where, I = intensity

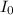`I_(0)`=Original intensity

Put the value into the formula

`120=10log_(10)((I)/(10^(-12)))`

`(120)/(10)=log_(10)((I)/(10^(-12)))`

`I=10^(12)*10^(-12)`

`I=1\ W/m^2`

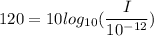
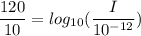
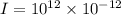
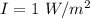
Hence, The intensity of the threshold of pain is 1 W/m²

Answer 2

Step-by-step explanation:

The intensity level is given by :

`dB=10\ log_(10)(I)/(I_o)`

`I_o=10^(-12)\ W/m^2`

The intensity of the threshold of pain is 120 decibels

`120=10\ log_(10)(I)/(10^(-12))`

`12=\ log_(10)(I)/(10^(-12))`

`10^(12)* 10^(-12)=I`

`I=1\ W/m^2`

So, the intensity of the threshold pain is 1 W/m². Hence, this is the required solution.