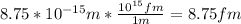Question

An alpha particle with a kinetic energy of 13.0 MeV makes a head-on collision with a gold nucleus at rest. part A: What is the distance of closest approach of the two particles? (Assume that the gold nucleus remains stationary and that it may be treated as a point charge. The atomic number of gold is 79, and an alpha particle is a helium nucleus consisting of two protons and two neutrons.)

Answer 1

8.75 fm

Step-by-step explanation:

We use this expression

`E=(Ze*(2e))/(4\pi \epsilon_(0) *d)`

Which is derived from conservation of energy. E is the kinetic energy. d is the distance to find, Ze and 2e are the charges of the gold nucleus and alpha particle respectively.
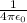`(1)/(4\pi \epsilon_(0) )` is the coulomb constant which is 9*10^9. Converting the energy to Joules

`13 MeV*(1 J)/(6.24*10^(12)MeV)=2.08*10^(-12) J`

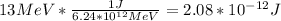
So, solving for distance (having all units in international system, distance ends up in meters)

`d=(9*10^9 *79*2*(1.6*10^(-19))^2)/(2.08*10^(-12)) = 8.75*10^(-15) m`

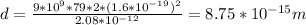
In fermi:

`8.75*10^(-15) m*(10^(15) fm)/(1 m)=8.75 fm`