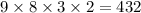Question

How many four-digit positive integers can be formed by using the digits from 1 to 9 so that two digits are equal to each other and the remaining two are also equal to each other but different from the other two ?

Answer 1

432

Explanation:

We are given that a four digit number can be formed by using digits from 1 to 9.

Two digits equal to each other and other two digits are equal to each other .

We have to find number of four digit numbers can be formed using digits from 1 to 9.

Total digits =9

Number of ways to filled first place =9

Number of ways to filled second place =1 because two digits are same

Number of ways to fill the third place =8 because different from previous two digits

Number of ways to fill the fourth place =1 because remaining two digits are same

Total number of ways to make four digit number =
`9* 1* 8* 1* {(4!)/(2!2!)}`

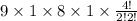
Because two digits out of 4 and remaining two digits are same select out of 4

Total number of ways in which four digit number can be formed=
`9* 8* 3* 2=432`