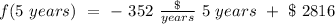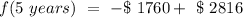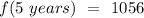Question

A computer is purchased for $2816 and depreciates at a constant rate to $0 in 8 years. Find a formula for the value, V , of the computer after t years have passed. Then use this formula to give the value of the computer after 5 years. (This is known as "straight-line depreciation" and is a depreciation model often used on tax forms).

Answer 1

• The formula its
  `f(t) \ = \ - \ 352 \ (\$ )/(years) \ t \ + \ \$ \ 2816`
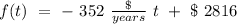
• After 5 years, the computer value its $ 1056

Step-by-step explanation:

Obtaining the formula

We wish to find a formula that

• Starts at 2816.
  `f(0 \ years) \ = \ \$ \ 2816`
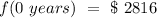
• Reach 0 at 8 years.
  `f( 8 \ years) \ = \ \$ \ 0`
• Depreciates at a constant rate. m

We can cover all this requisites with a straight-line equation. (an straigh-line its the only curve that has a constant rate of change) :

`f(t) \ = \ m\ t \ + \ b`,

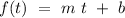where m its the slope of the line and b give the place where the line intercepts the y axis.

So, we can use this formula with the data from our problem. For the first condition:

`f ( 0 \ years ) = m \ (0 \ years) + b = \$ \ 2816`

`b = \$ \ 2816`

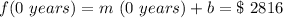
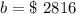
So, b = $ 2816.

Now, for the second condition:

`f ( 8 \ years ) = m \ (8 \ years) + \$ \ 2816 = \$ \ 0`

`m \ (8 \ years) = \ - \$ \ 2816`

`m = (\ - \$ \ 2816)/(8 \ years)`

`m = (\ - \$ \ 2816)/(8 \ years)`

`m = \ - \ 352 (\$ )/(years)`

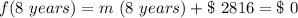
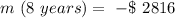
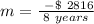
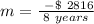
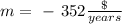
So, our formula, finally, its:

`f(t) \ = \ - \ 352 \ (\$ )/(years) \ t \ + \ \$ \ 2816`

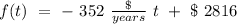
After 5 years

Now, we just use t = 5 years in our formula

`f(5 \ years) \ = \ - \ 352 \ (\$ )/(years) \ 5 \ years \ + \ \$ \ 2816`

`f(5 \ years) \ = \ - \$ \ 1760 + \ \$ \ 2816`

`f(5 \ years) \ = $ \ 1056`