Question

Radon is a gas produced when radium decays, and it can enter homes where it can be a health threat. Among 180 homes in Hyde Park, 25 were found to have unsafe radon levels. Among 230 homes in LaGrange, 50 were found to have unsafe radon levels. Use a .05 significance level to test that the two towns have different rates of unsafe radon levels. Use our 4 step procedure.

Answer 1

We are given that Among 180 homes in Hyde Park, 25 were found to have unsafe radon levels. Among 230 homes in La Grange, 50 were found to have unsafe radon levels.

Claim : the two towns have different rates of unsafe radon levels.

Let
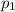`p_1` and
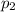`p_2`be the rates of unsafe radon levels of Hyde Park and LaGrange respectively .

`H_0:p_1=p_2\\H_a:p_1\\eq p_2`

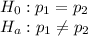
Among 180 homes in Hyde Park, 25 were found to have unsafe radon levels

So,
`n_1=180, y_1=25`

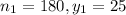
Among 230 homes in La Grange, 50 were found to have unsafe radon levels.

So,
`n_2=230, y_2=50`

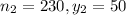
We will use Comparing Two Proportions

`\widehat{p_1}=(y_1)/(n_1)`

`\widehat{p_1}=(25)/(180)`

`\widehat{p_1}=0.1388`

`\widehat{p_2}=(y_2)/(n_2)`

`\widehat{p_2}=(50)/(230)`

`\widehat{p_2}=0.217`

`\widehat{p}=(y_1+y_2)/(n_1+n_2) =(25+50)/(180+230)=0.1829`

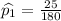
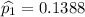
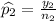
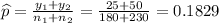
Formula of test statistic :
`\frac{\widehat{p_1}-\widehat{p_2}}{\sqrt{\widehat{p}(1-\widehat{p})((1)/(n_1)+(1)/(n_2))}}`

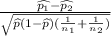
Substitute the values

test statistic :
`\frac{0.138-0.217}{\sqrt{0.1829(1-0.1829)((1)/(180)+(1)/(230))}}`

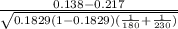
test statistic : −2.053

Refer the z table for p value

p value = 0.0202

α= 0.05

Since p value < α

So, we reject the null hypothesis that the two towns have same rates of unsafe radon levels.

So, Claim is true.