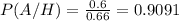Answer:
(a) The probability is 0.66
(b) The probability is 0.9091
Explanation:
The probability that the target is hit by either A or B is calculated as the sum of the probability that the target is hit by A and the probability that the target is hit by B less the probability that A and B happens, as:
P = 0.6 + 0.15 - 0.6(0.15) = 0.6 + 0.15 - 0.09 = 0.66
On the other hand, the probability that the target is hit by A knowing that it is hit is calculated as:
P(A/H) = P(A∩H)/P(H)
Where P(H) is the probability that the target is hit by either A or B and P(A∩H) is the probability that the target is hit by A.
So,