Question

Geometry: what is the perimeter of XYZ?

Answer 1

The perimeter is
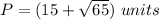`P=(15+√(65))\ units` or
`P=23.06\ units`

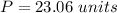
Explanation:

we know that

The perimeter of triangle XYZ is equal to the sum of its length sides

`P=XY+YZ+XZ`

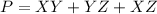
the formula to calculate the distance between two points is equal to

`d=\sqrt{(y2-y1)^(2)+(x2-x1)^(2)}`

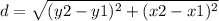
we have

`X(0,2),Y(3,-2),Z(-7,-2)`

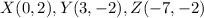
step 1

Find the distance XY

`X(0,2),Y(3,-2)`

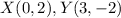
substitute the values in the formula

`d=\sqrt{(-2-2)^(2)+(3-0)^(2)}`

`d=\sqrt{(-4)^(2)+(3)^(2)}`

`d=√(25)`

`dXY=5\ units`

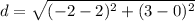
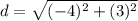
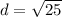
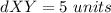
step 2

Find the distance YZ

`Y(3,-2),Z(-7,-2)`

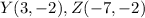
substitute the values in the formula

`d=\sqrt{(-2+2)^(2)+(-7-3)^(2)}`

`d=\sqrt{(0)^(2)+(-10)^(2)}`

`d=√(100)`

`dYZ=10\ units`

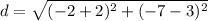
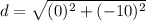
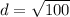
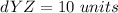
step 3

Find the distance XZ

`X(0,2),Z(-7,-2)`

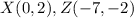
substitute the values in the formula

`d=\sqrt{(-2-2)^(2)+(-7-0)^(2)}`

`d=\sqrt{(-4)^(2)+(-7)^(2)}`

`dXZ=√(65)\ units`

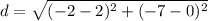
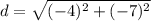
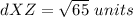
step 4

Find the perimeter

`P=XY+YZ+XZ`

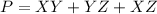
substitute

`P=5+10+√(65)`

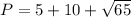
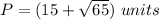`P=(15+√(65))\ units` ----> exact value

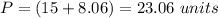`P=(15+8.06)=23.06\ units` -----> approximate value