Question

Light propagating in air strikes the surface of a lake. The reflected ray makes 62° angle with the normal. What angle does the refracted ray in the water makes with the normal. (Hint: index of refraction for water 1.33) (a) 420 (b) 48° (c) 540 (d) 58° me= 9.11 × 10-31 kg 80-8.85 x 10-12 C/N.m2 h= 6.63 × 10-34 J-s m,-1.67 x 10-27 kg k-8.988 10 N -m/C e= 1.6× 10-19c o4t x 10-7 N/A Pa 1.69 × 10-4 Ω-m.

Answer 1

(a) 42°

Step-by-step explanation:

According to the law of reflection:

Angle of incidence = Angle of reflection

So, angle of reflection = 62°

Angle of incidence = 62°

For refraction,

Using Snell's law as:

`n_i* {sin\theta_i}={n_r}*{sin\theta_r}`

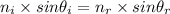
Where,

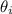`{\theta_i}` is the angle of incidence ( 62.0° )

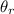`{\theta_r}` is the angle of refraction ( ? )

`{n_r}` is the refractive index of the refraction medium (water, n=1.33)

`{n_i}` is the refractive index of the incidence medium (air, n=1)

Hence,

`1* {sin62.0^0}={1.33}*{sin\theta_r}`

Angle of refraction =
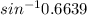`sin^(-1)0.6639` = 42°