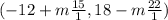Question

Solve the Diophantine equations: (2.a) 21x + 15y = 6 (2.b) 22u + 15v = 6

Answer 1

The particular solution of 2.a is
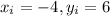`x_(i)=-4, y_(i)=6` and the complete solution is
`x=-4+5m, y=6-7m`.

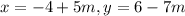The particular solution of 2.b is
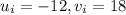`u_(i)=-12, v_(i)=18` and the complete solution is
`u=-12+15m, v=18-22m`

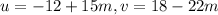
Explanation:

The Diophantine equation ax+by=n has solutions if and only if gcd(a,b) | n. If this is true, it has infinitely many solutions, and any solution can be used to generate a complete solution.

This are the steps that you need to follow:

• Use the Euclidean algorithm to compute gcd(a,b)=d

So for the equation
`21x+15y=6`,

`21=1*15+6\\15=2*6+3\\6=2*3+0`

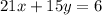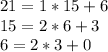
When the remainder r = 0, the gcd is the divisor, 3, in the last equation so gcd(21,15) = 3

Then, observe that 3|6 (that means when we divide 6 by 3, the remainder is 0.) is true therefore there are integer solutions to the equation.

The same for the equation
`22u+15v=6`,

`22=1*15+7\\15=2*7+1\\7=7*1+0`

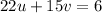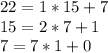
When the remainder r = 0, the gcd is the divisor, 1, in the last equation so gcd(22,15) = 1 and 1|6 is true therefore there are integer solutions to this equation.

• The next step is reformat the equations from the Euclidean algorithm as follows:

For the equation
`21x+15y=6`

`6=21-1*15\\3=15-2*6`

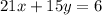
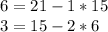
For the equation
`22u+15v=6`

`1=15-2*7\\7=22-1*15`

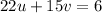
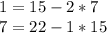
• Using substitution, go through the steps of the Euclidean algorithm to find a solution to the equation ax_{i}+by_{i}=d

For the equation
`21x_(i)+15y_(i)=3`

`3=15-2*6\\3=15-2(21-1*15)\\3=(3*15)+(-2*21)\\3=21*(-2)+15*3`

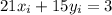
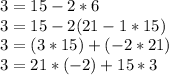
This gives x_i=-2 and y_i=3 as a solution to the equation
`21x_(i)+15y_(i)=3`

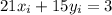
For the equation
`22u+15v=1`

`1=15-2*7\\1=15-2*(22-1*15)\\1=3*15+(-2*22)\\1=22*(-2)+15*3`

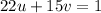
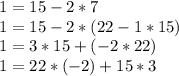
This gives u_i=-2 and v_i=3 as a solution to the equation
`22u_(i)+15v_(i)=1`

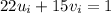
• The initial solution to the equation ax+by=n is the ordered pair
  `(x_(i)*(n)/(d),y_(i)*(n)/(d) )`

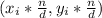
Then an initial solution to the equation
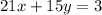`21x+15y=3` is

`x_(i)=(-2*(6)/(3))=-4\\y_(i)=(3*(6)/(3))=6`

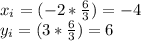
For the equation
`22u+15v=1`

`u_(i)=(-2*(6)/(1))=-12\\v_(i)=(3*(6)/(1))=18`

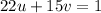
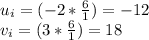
• Find the complete solutions of the equation ax+by=n

For this you can use this Theorem:

if
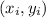`(x_(i),y_(i))` is an integer solution of the Diophantine equation ax+by=n, then all integer solutions to the equation are of the form

`(x_(i) +m(b)/(gcd(a,b)) ,y_(i) -m(a)/(gcd(a,b)))`

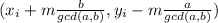
for some integer m.

The complete solutions for the equation
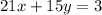`21x+15y=3` are:

`(-4 +m(15)/(3) ,6 -m(21)/(3))`

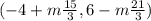
The complete solutions for the equation
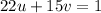`22u+15v=1` are:

`(-12 +m(15)/(1) ,18 -m(22)/(1))`