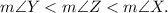Answer:
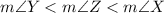
Explanation:
In triangle XYZ, the lengths of sides are
If
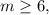 then
then
and
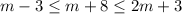
The greatest angle is opposite to the greatest side, the smallest angle is opposite to the smallest side, so
- the greatest side is
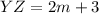 - the greatest angle is
- the greatest angle is
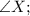
- the smallest side is
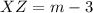 - the smallest angle is
- the smallest angle is

Thus,