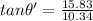Question

A train at a constant 79.0 km/h moves east for 27.0 min, then in a direction 50.0° east of due north for 29.0 min, and then west for 37.0 min. What are the (a) magnitude and (b) angle (relative to east) of its average velocity during this trip?

Answer 1

Magnitude of avg velocity,
`|v_(avg)| = 18.9 km/h`

`\theta' = 56.85^(\circ)`

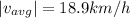
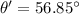
Given:

Constant speed of train, v = 79 km/h

Time taken in East direction, t = 27 min =
`(27)/(60) h`

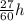
Angle,
`\theta = 50^(\circ)`

Time taken in
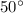`50^(\circ)`east of due North direction, t' = 29 min =
`(29)/(60) h`

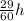
Time taken in west direction, t'' = 37 min =
`(27)/(60) h`

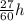
Solution:

Now, the displacement, 's' in east direction is given by:

`\vec{s} = vt = 79* (27)/(60) = 35.5\hat{i} km`

Displacement in
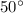`50^(\circ)` east of due North for 29.0 min is given by:

`\vec{s'} = vt'sin50^(\circ)\hat{i} + vt'cos50^(\circ)\hat{j}`

`\vec{s'} = 79((29)/(60))sin50^(\circ)\hat{i} + 79((29)/(60))cos50^(\circ)\hat{j}`

`\vec{s'} = 29.25\hat{i} + 24.54\hat{j} km`

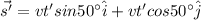
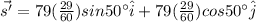
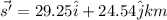
Now, displacement in the west direction for 37 min:

`\vec{s''} = - vt''hat{i} = - 79(37)/(60) = - 48.72\hat{i} km`

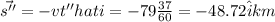
Now, the overall displacement,

`\vec{s_(net)} = \vec{s} + \vec{s'} + \vec{s''}`

`\vec{s_(net)} = 35.5\hat{i} + 29.25\hat{i} + 24.54\hat{j} - 48.72\hat{i}`

`\vec{s_(net)} =  16.03\hat{i} + 24.54\hat{j} km`

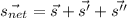
(a) Now, average velocity,
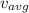`v_(avg)` is given:

`v_(avg) = \frac{total displacement, \vec{s_(net)}}{total time, t}`

`v_(avg) = \frac{16.03\hat{i} + 24.54\hat{j}}{(27 + 29 + 37)/(60)}`

`v_(avg) = 10.34\hat{i} + 15.83\hat{j}) km/h`

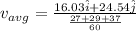
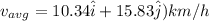
Magnitude of avg velocity is given by:

`|v_(avg)| = \sqrt{(10.34)^(2) + (15.83)^(2)} = 18.9 km/h`

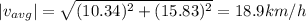
(b) angle can be calculated as:

`tan\theta' = (15.83)/(10.34)`

`\theta' = tan^(- 1)(15.83)/(10.34) = 56.85^(\circ)`