Question

Report Error Find the sum of the series 1 + \frac{1}{2} + \frac{1}{10} + \frac{1}{20} + \frac{1}{100} + \cdots, where we alternately multiply by \frac 12 and \frac 15 to get successive terms.

Answer 1

The sum of given series is 5/3.

Explanation:

Given series is

`1+(1)/(2)+(1)/(10)+(1)/(20)+(1)/(100)+...`

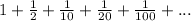
We need to find the sum of above series. In this series we alternately multiply by 1/2 and 1/5 to get successive terms.

Isolate the odd and even place terms.

`(1+(1)/(10)+(1)/(100)+...)+((1)/(2)+(1)/(20)+...)`

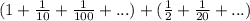
Now, we have two infinite series.

Sum of an infinite GP is

`S_\infty=(a)/(1-r)`

where, r is first term and r is common ratio, 0 < r < 1.

In
`1+(1)/(10)+(1)/(100)+...`

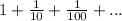
First term = 1

Common ratio = 1/10

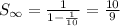
`S_\infty=(1)/(1-(1)/(10))=(10)/(9)`

In
`(1)/(2)+(1)/(20)+...`

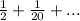
First term = 1/2

Common ratio = 1/10

`S_\infty=((1)/(2))/(1-(1)/(10))=(5)/(9)`

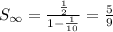
The sum of given series is

`S_\infty=(10)/(9)+(5)/(9)`

`S_\infty=(15)/(9)`

`S_\infty=(5)/(3)`

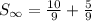
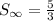
Therefore the sum of given series is 5/3.