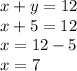Question

Traveling with the current a certain boat went 12 km/h. Against the same current it only went 2 km/h. Find the speed of the boat in still water and the speed of the current.

Answer 1

5, 7

Explanation:

Answer 2

The speed of the boat is 7 km/h and thes peed of the current is 5 km/h;

Explanation:

We don't know neither the speed of the boat nor the speed of the current, so let:

speed of the boat = x;

speed of the current = y;

If the boat is travelling with the current we know that those two speed are adding up, therefore we can conclude that:

x + y = 12;

But If the boat is travelling against the current we know that we have to subtract them, therefore:

x - y = 2;

Now we've a system of equations with the same two variables, therefore, by substitution method (or any other method) we can find the variables:

`\left \{ {{x +y = 12} \atop {x - y = 2}} \right.`

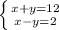
So using the first equation, we get that:

`x = 12 - y`

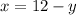
And substituting that x to the second equation we get:

`x - y = 2\\(12 - y) - y = 2\\12 - 2y = 2\\12 - 2 = 2y\\10 = 2y\\5 = y`

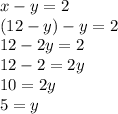
So we can conclude that the speed of the current is 5 km/h.

And now with that answer, using equation 1, we can solve the speed of the boat.

`x + y = 12\\x + 5 = 12\\x = 12 -5\\x = 7`