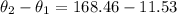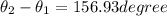Question

Two particles execute simple harmonic motion of the same amplitude and frequency along close parallel lines. They pass each other moving in opposite directions each time the displacement of the first particle is 1/5 of its amplitude. What is their phase difference?

Answer 1

`\theta_2 - \theta_1 = 156.93 degree`

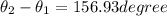
Step-by-step explanation:

As we know that the displacement of the particle from the mean position is 1/5 times of its amplitude

so we have

`y = A sin\omega t`

`y = (A)/(5)`

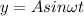
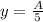
so now we have

`(A)/(5) = A sin\omega t`

now we have

`\theta_1 = 11.53 degree`

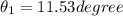
so the phase other particle in opposite direction is given as

`\theta_2 = 180 - 11.53 = 168.46 degree`

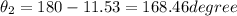
so we have phase difference given as

`\theta_2 - \theta_1 = 168.46 - 11.53`

`\theta_2 - \theta_1 = 156.93 degree`