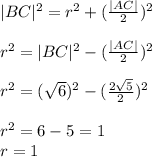Answer:
r=1
Explanation:
First we need to know the length of each side of the triangle, so we use the formula of the vector modulus:
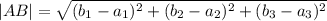
By doing so, we find:
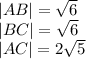
With this we know that the triangle is not right, but, we assume the longest side as the hypotenuse of the problem.
As we have two equal sides, we know that the line between point |AB| and the center of the hypotenuse is perpendicular, therefore, we can calculate it using Pythagoras theorem: