Question

Use the Euler method with dx=1/4 to estimate y ( 2 ) if y' = x sine y and y ( 0 ) = 8. What is the exact value of y ( 2 )​?

Answer 1

y(2) = 8.248

Explanation:

y(2) is the value of y when x = 2.

f(x,y) = y' = x sine y

`y_(0) = 8, x_(0) = 0`

--------------------------------

`y_(1) = y_(0) + 0.25*f(x_(0),y_(0)) = 8 + 0 = 8`

`x_(1) = x_(0) + dx = 0.25`

-----------------------------------

`y_(2) = y_(1) + 0.25*f(x_(1),y_(1)) = 8+0.25*f(0.25,8) = 8 +8.7*10^(-3) = 8.008`

`x_(2) = x_(1) + dx = 0.25 + 0.25 = 0.50`

----------------------------------

`y_(3) = y_(2) + 0.25*f(x_(2),y_(2)) = 8.008+0.25*f(0.50,8.008) = 8.008 + 0.02 = 8.028`

`x_(3) = x_(2) + dx = 0.50 + 0.25 = 0.75`

-----------------------------------

`y_(4) = y_(3) + 0.25*f(x_(3),y_(3)) = 8.028+0.25*f(0.75,8.028) = 8.028 + 0.026 = 8.054`

`x_(4) = x_(3) + dx = 0.75 + 0.25 = 1`

-----------------------------------

`y_(5) = y_(4) + 0.25*f(x_(4),y_(4)) = 8.054+0.25*f(1,8.054) = 8.054 + 0.035 = 8.089`

`x_(5) = x_(4) + dx = 1 + 0.25 = 1.25`

-----------------------------------

`y_(6) = y_(5) + 0.25*f(x_(5),y_(5)) = 8.089+0.25*f(1.25,8.089) = 8.089 + 0.044 = 8.133`

`x_(6) = x_(5) + dx = 1.25 + 0.25 = 1.50`

-----------------------------------

`y_(7) = y_(6) + 0.25*f(x_(6),y_(6)) = 8.133+0.25*f(1.50,8.133) = 8.133 + 0.053 = 8.186`

`x_(7) = x_(6) + dx = 1.50 + 0.25 = 1.75`

-----------------------------------

`y_(8) = y_(7) + 0.25*f(x_(7),y_(7)) = 8.186+0.25*f(1.75,8.186) = 8.186+ 0.062 = 8.248`

`x_(8) = x_(7) + dx = 1.75 + 0.25 = 2`

----------------------------------

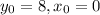
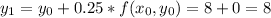
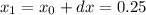
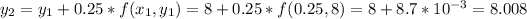
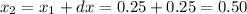
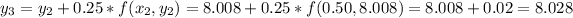
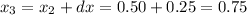
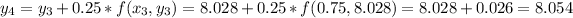
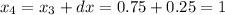
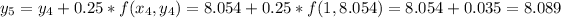
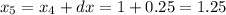
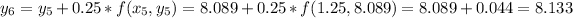
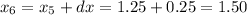
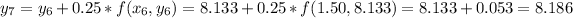
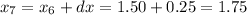
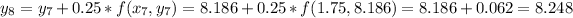
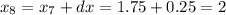
So, after 8 iterations at the Euler's method, we arrive at the moment x = 2. At this moment, we have that y = 8.248. So, y(2) = 8.248