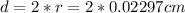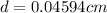Question

A fuse in an electric circuit is a wire that is designed to melt, and thereby open the circuit, if the current exceeds a predetermined value. Suppose that the material to be used in a fuse melts when the current density rises to 350 A/cm2. What diameter of cylindrical wire should be used to make a fuse that will limit the current to 0.58 A?

Answer 1

0.04594 cm

Step-by-step explanation:

So, we need the wire melt when the max current density its
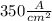`350 (A)/(cm^2)`. Now, we got our limit current, 0.58 A.

The current density its
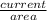`(current)/(area)`, so, with our data, we can obtain the cross area of the wire.

For a cylinder, the area its given by:

`area =\pi r^2`

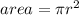
We can put all this in the equation for the max current density:

`density_(max) =(current_(limit))/(area)`

`density_(max) =(current_(limit))/(\pi r^2)`

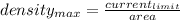
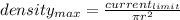
And now, we can work it a little:

`r^2 =(current_(limit))/(\pi * density_(max))`

`r =\sqrt{ (current_(limit))/(\pi * density_(max))`

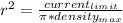
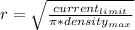
using our values, max current density =
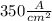`350 (A)/(cm^2)` , and limit current = 0.58 A,

`r =\sqrt{ (0.58 A)/(\pi * 350 (A)/(cm^2) )}`

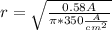
And, of course, the diameter its two times the radius:

`d = 2 * r = 2 * 0.02297 cm`

`d = 0.04594 cm`