Question

A string along which waves can travel is 4.36 m long and has a mass of 222 g. The tension in the string is 60.0 N. What must be the frequency of traveling waves of amplitude 6.43 mm for the average power to be 50.4 W?

Answer 1

frequency is 195.467 Hz

Step-by-step explanation:

given data

length L = 4.36 m

mass m = 222 g = 0.222 kg

tension T = 60 N

amplitude A = 6.43 mm = 6.43 ×
`10^(-3)` m

power P = 54 W

to find out

frequency f

solution

first we find here density of string that is

density ( μ )= m/L ................1

μ = 0.222 / 4.36

density μ is 0.050 kg/m

and speed of travelling wave

speed v = √(T/μ) ...............2

speed v = √(60/0.050)

speed v = 34.64 m/s

and we find wavelength by power that is

power = μ×A²×ω²×v / 2 ....................3

here ω is wavelength put value

54 = ( 0.050 ×(6.43 ×
`10^(-3)`)²×ω²× 34.64 ) / 2

0.050 ×(6.43 ×
`10^(-3)`)²×ω²× 34.64 = 108

ω² = 108 / 7.160 ×
`10^(-5)`

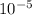
ω = 1228.16 rad/s

so frequency will be

frequency = ω / 2π

frequency = 1228.16 / 2π

frequency is 195.467 Hz