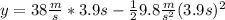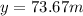Question

A slingshot can project a pebble at a speed as high as 38.0 m/s. (a) If air resistance can be ignored, how high (in m) would a pebble launched at this speed rise if projected straight up?

Answer 1

73.67 m

Step-by-step explanation:

If projected straight up, we can work in 1 dimension, and we can use the following kinematic equations:

`y(t) = y_0 + V_0 * t + (1)/(2) a t^2`

`V(t) = V_0 + a * t`,

Where
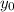`y_0` its our initial height,
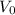`V_0` our initial speed, a the acceleration and t the time that has passed.

For our problem, the initial height its 0 meters, our initial speed its 38.0 m/s, the acceleration its the gravitational one ( g = 9.8 m/s^2), and the time its uknown.

We can plug this values in our equations, to obtain:

`y(t) =  38 (m)/(s) * t - (1)/(2) g t^2`

`V(t) = 38 (m)/(s) - g * t`

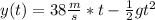
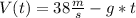
note that the acceleration point downwards, hence the minus sign.

Now, in the highest point, velocity must be zero, so, we can grab our second equation, and write:

`0 m = 38 (m)/(s) - g * t`

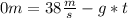
and obtain:

`t = 38 (m)/(s) / g`

`t = 38 (m)/(s) / 9.8 (m)/(s^2)`

`t = 3.9 s`

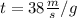
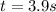
Plugin this time on our first equation we find:

`y = 38 (m)/(s) * 3.9 s - (1)/(2) 9.8 (m)/(s^2) (3.9 s)^2`

`y=73.67 m`