Question

A frame of mass m, when suspended from a coil spring, stretches the spring by h. A lump of putty of mass mp is dropped from rest onto the frame from a height of H. Find the maximum distance the frame moves downward from its initial equilibrium position.

Answer 1

Hi!

If you have a spring with elastic constant k, the force needed to stretch it

x is given by F = k*x

When the frame is suspended the force is its wheight: F = g*m

Then, g*m = k*h, and you can get k = g*m/h

When the lump of putty falls a distance H, its potential energy is converted into kinetic energie, so:

`mgH = (m_p)/(2) V^2`
`E_(potential) = - mgD + (k)/(2) D^2`

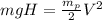
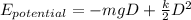
where V is velocity. With that velocity the lump collides with the frameand gets sticked. The conservation of momentum gives you the velocity V' of the frame with the lump sticked, whos mass is (m + mp). Conservation of momentum is expressed in the equation:

V*mp = V' * (m + mp)

The frame+lump system has now a kinetic energy:

`E_k = (m + mp)/(2) V'^2`

It is going to move downwards until al the kinetic energy is transformed into potential energy, elastic and gravitational :

`E_(potential) = -(m+mp)gD + (k)/(2)D^2 = ((m+mp))/(2) V'^2 = (m^2)/(2(m+mp))  V^2`