Question

ABC Bank pays 9% simple interest on its savings account balances, whereas XYZ Bank pays 9% interest compounded annually. If you made a deposit of $7,500 in each bank, how much more money would you earn from your XYZ Bank account at the end of eight years?

Answer 1

The answer is $2,044.22.

Step-by-step explanation:

We can simply calculate the final value of investing in each of the banks, and then calculate the difference between those values to see how much more money you would earn from investing in bank XYZ.

The formula for calculating the value of an investment with simple interest rate is given by:

`V_(s)(n)=P* R* n+P = P (1+R* n)`

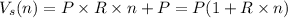
Where:

P is the principal,

R is the interest rate,

n is the number of years.

Therefore, if bank ABC is chosen, the final value of the investment would be:

`V_(ABC)(8)= 7500* (1+0,09* 8)= 7500* (1.72)= 12900`

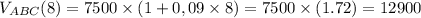
Now, the formula for calculating the value of an investment with annually compound interest is given by:

`V_(c)(n)=(1+R)^nP`

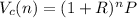
Therefore, if we choose to invest in bank XYZ, the value we'd obtain at the end of 8 years with a 9% interest rate would be:

`V_(XYZ)(8)=7500 * (1+0.09)^8 = 14944.22`

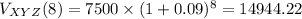
The difference between investing in bank XYZ and bank ABC is:

`V_(XYZ)-V_(ABC) =14944.22-12900=2044.22`

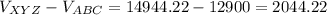
Therefore if you invest in bank XYZ you'd earn $2,044.22 more at the end of eight years, than if you'd invest in bank ABC.