Question

If the volume of a cube is increased by a factor of 10 (so that the new volume is 10 times the size of the original volume), by what factor does the surface area of the cube change?

Answer 1

surface area of cube
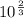`10^{(2)/(3) }` time

Explanation:

given data

new volume = 10 time original volume

to find out

what factor surface area change

solution

we consider here side of cube is a

and volume is V

we consider here a is 2

then volume will be v1 = a³ = 2³ = 8

and surface area = 6a² = 6(2)² = 24 ..........1

so if volume increase 10 time

than

V = 10 × v1

a³ = 10 × 8

a³= 80

a = 2 × ∛10

and

surface area increase here

surface area = 6a²

surface area = 6( 2 × ∛10 )²

surface area = 24 ×
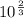`10^{(2)/(3) }` ............2

so from equation 1 and 2

surface area / surface area = 24 ×
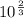`10^{(2)/(3) }` / 24

surface area =
`10^{(2)/(3) }`

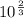
so here surface area of cube will be
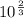`10^{(2)/(3) }` time