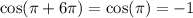A whole turn around the circumference is an angle of 2pi.
So, two turns are 4pi, and three turns are 6pi.
With every turn the trigonometric functions reset, because you keep visiting the same points along the circumference.
This is why we have
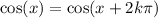
i.e. the value of a trigonometric function (in this case the cosine) doesn't change if you add another turn around the circumference.
In this case, we have
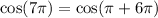
i.e. an angle of 7pi means to make 3 turns around the circle, and then an additional angle of pi. Since the 3 turns are irrelevant, we finally have