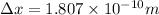Question

The speed of a certain proton is 350 km/s. If the uncertainty in its momentum is 0.100%, what is the necessary uncertainty in its location?

Answer 1

`\Delta x = 1.807 * 10^(-10)m`

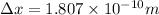
Step-by-step explanation:

mass of proton, m = 1.67 x 10^-27 kg

speed of proton, v = 350 km/s = 350,000 m/s

Momentum of proton, p = mass x speed

p = 1.67 x 10^-27 x 350000 = 5.845 x 10^-22 kg m /s

uncertainty in momentum, Δp = 0.1 % of p

Δp =
`(0.1* 5.845 * 10^(-22))/(100)=5.845 * 10^(-25)`

According to the principle

`\Delta x* \Delta p \geq  (h)/(2\pi )`

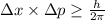
where, Δx be the uncertainty in position

`\Delta x* 5.845 * 10^(-25)=  (6.634 * 10^(-34))/(2* 3.14)`

`\Delta x = 1.807 * 10^(-10)m`