Answer:
First equation is -425
Second equation is 11.25
Explanation:
First equation we can write as
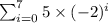
computing
When i=0 ->
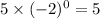
When i=1 ->
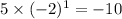
...
When i=7 ->
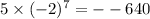
then replacing each term we have
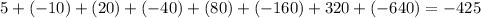
For the second equation we'll have 9 terms, solving in a similar fashion
When i=1 ->
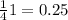
When i=2 ->
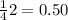
When i=3 ->
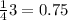
...
When i=9 ->
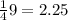
So we have 0.25 + 0.50 + 0.75 + 1.00 + 1.25 + 1.50+ 1.75 +2.00 +2.25