Question

Please help! ONLY REAL ANSWERS. You will get reported and points taken away if you answer falsely or “idk the answer).

Answer 1

A quadratic function generally does not have an inverse except on a restricted domain. If the domain of the original function is restricted to x ≥ 0, then the inverse function is ...

`f^(-1)(x)=\displaystyle\sqrt{(x-4)/(5)}`

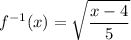
Explanation:

Start by interchanging x and "y", then solve for y.

y = 5x² +4 . . . . . . given

x = 5y² +4 . . . . . . with x and y interchanged

x -4 = 5y² . . . . . . subtract 4

(x -4)/5 = y² . . . . . divide by 5

√((x -4)/5) = y . . . take the square root . . . . x ≥ 4, y ≥ 0

Then, ...

`f^(-1)(x)=\displaystyle\sqrt{(x-4)/(5)}`

_____

The graph shows the original f(x) and the "inverse", called f1(x). Note that it is only a reflection across y=x of the right half of the original function. That is, the inverse only exists for the original function when its domain is restricted to x ≥ 0. (The domain of the inverse function is x ≥ 4.)