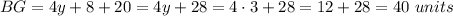Answer:
40 units
Explanation:
The midpoint of the segment is the point on that line segment that divides the segment into two congruent segments.
If I is the midpoint of the segment BG, then segments BI and IG are congruent segments.
BI = 4y + 8 units
IG = 20 units
Hence,

The segment additional postulate states that if we are given two points on a line segment, B and G, a third point I lies on the line segment BG if and only if the distances between the points meet the requirements of the equation
BI + IG = BG.
So,