Question

In how many ways can 10 people be divided into three groups, one group with 4 people and the other two groups with 3 people each?

Answer 1

There are 4200 ways

Explanation:

The number of ways in which n elements can be organized in k groups is calculated as:

`(n!)/(n_1!*n_2!*...*n_k!)`

Where n is the number of elements and
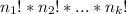`n_1!*n_2!*...*n_k!` are the number of elements of each group.

In this case, we have 10 people to create 3 groups, one with 4 people, and two groups with 3 people. So, n is equal to 10, k is equal to 3,
`n_1` is equal to 4,
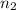`n_2` is equal to 3 and
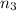`n_3` is equal to 3.

Then, replacing the values, we get:

`(10!)/(4!*3!*3!)=4,200`

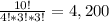
So, there are 4,200 ways to divided 10 people into three groups.