Question

A piece of wire 25 m long is cut into two pieces. One piece is bent into a square and the other is bent into an equilateral triangle.(a) How much wire should be used for the square in order to maximize the total area

Answer 1

10.87 m

Step-by-step explanation:

Total length of the wire = 25 m

Let the length of one piece is y and other piece is 25 - y

Let the side of square is a.

So, 4 a = y

a = y / 4

And the side of triangle is b

3 b = (25 - y)

b = (25 - y) / 3

Area of square, A1 = side x side =

A1 = y² / 16

Area of equilateral triangle, A2 =
`(√(3))/(4)* b^(2)`

`A_(2)=(√(3))/(4)(\left ( 25-y \right )^(2))/(9)`

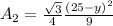
Total area, A = A1 + A2

`A=(y^(2))/(16)+(√(3))/(4)(\left ( 25-y \right )^(2))/(9)`

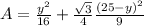
For maxima and minima, fins dA /dy

`(dA)/(dy)=(y)/(8)-(1.732)/(18) * (25-y)/(1)`

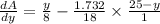
It is equal to zero.

`(y)/(8)=(1.732)/(18) * (25-y)/(1)`

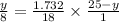
9y = 173.2 -6.928 y

15.928 y = 173.2

y = 10.87 m

So, the length of wire to make square is 10.87 m.