Answer:


Explanation:
The given equation is:
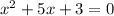
To find the solution of any quadratic equation we use:
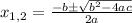
Where:
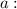 is the coefficient of the quadratic term.
is the coefficient of the quadratic term.
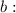 is the coefficient of the linear term.
is the coefficient of the linear term.
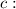 is the independent term.
is the independent term.
So, according to this, each variables is equal to:

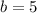
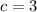
Now, we substitute these values in the formula:
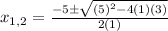

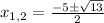
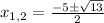
So, one solution has the positive sign, and the other the negative sign. Therefore the solutions are:
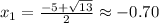

As you can see, the solution was founded just by using the formula, identifying the values of a, b and c. Then, solving the formula we all values replaced.