Question

Two vectors, r and c, are equal: r = c. Which of the following statements are true? (Select all that apply.)

(A) the y-component of r must be equal to the y-component of c
(B) the x-component of r must be equal to the x-component of c
(C) the z-component of r must be equal to the z-component of c
(D) The directions of r and c may be different
(E) The magnitudes of r and c may be different
(F) The unit vector r must be equal to the unit vector c.

Answer 1

(A) The y-component of r must be equal to the y-component of c

(B) The x-component of r must be equal to the x-component of c

(C) The z-component of r must be equal to the z-component of c

(F) The unit vector r must be equal to the unit vector c.

Step-by-step explanation:

If two vectors are equal there are some conditions must be satisfy for the two vectors to be equal.

Let us suppose 2 vectors as,

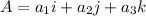`A=a_(1)i+ a_(2)j+a_(3)k` and

`B=b_(1)i+ b_(2)j+b_(3)k`

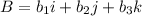
The conditions for the above two vectors should be equal are:

(1)
`a_(1)=b_(1)`,
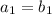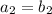`a_(2)=b_(2)`, and
`a_(3)=b_(3)`.

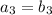(2) Unit vector of A must be equal to unit vector of B.

(3) Magnitude of both the vectors should be equal.

Now, according to question and observing above conditions of equality for r and c to be equal, the statements should be true are:

(A) The y-component of r should be equal to the y-component of c

(B) The x-component of r should be equal to the x-component of c

(C) The z-component of r should be equal to the z-component of c

(F) The unit vector r should be equal to the unit vector c.