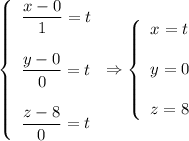Question

Find a vector parametrization for the line with the given description. Perpendicular to the yz-plane, passes through (0, 0, 8)

Answer 1

`\left\{\begin{array}{l}x=t\\ \\y=0\\ \\z=8\end{array}\right.`

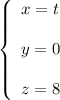
or

`\overrightarrow{(t,0,8)}`

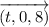
Explanation:

yz-plane has the equation
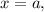`x=a,` where
`a` is a real constant. The normal vector of this plane (vector perpendicular to the plane) is

`\overrightarrow {n}=(1,0,0)`

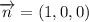
If the line is perpendicular to this plane, then it is parallel to the normal vector, so the equation of this line is

`(x-x_0)/(1)=(y-y_0)/(0)=(z-z_0)/(0),`

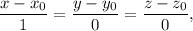
where
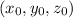`(x_0,y_0,z_0)` are coordinates of the point the line is passing through.

In your case, the line is passing through the point (0,0,8), so the canonical equation of the line is

`(x-0)/(1)=(y-0)/(0)=(z-8)/(0)`

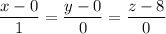
Write a vector parametrization for this line

`\left\{\begin{array}{l}(x-0)/(1)=t\\ \\(y-0)/(0)=t\\ \\(z-8)/(0)=t\end{array}\right.\Rightarrow \left\{\begin{array}{l}x=t\\ \\y=0\\ \\z=8\end{array}\right.`