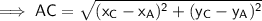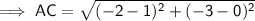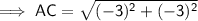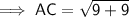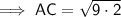Answer:
a) OA = 1 unit
b) BC = 3 units
c) OD = 2 units
d) AC = 3√2 units
Explanation:
Given function:
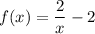
Part (a)
Point A is the x-intercept of the curve.
To find the x-intercept of the curve (when y = 0), set the function to zero and solve for x:
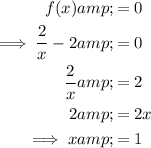
Therefore, A (1, 0) and so OA = 1 unit.
Part (b)
If OB = 2 units then B (-2, 0). Therefore, the x-value of Point C is x = -2.
To find the y-value of Point C, substitute x = -2 into the function:
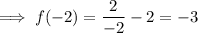
Therefore, C (-2, -3) and so BC = 3 units.
Part (c)
Asymptote: a line that the curve gets infinitely close to, but never touches.
The y-value of Point D is the horizontal asymptote of the function.
The function is undefined when x = 0 and therefore when y = -2.
Therefore, D (0, -2) and so OD = 2 units.
Part (d)
From parts (a) and (c):
To find the length of AC, use the distance between two points formula:
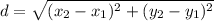
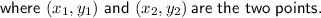
Therefore: