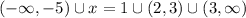Question

Solve the given inequality :


`\begin{gathered}\sf \: \frac{ {(x - 1)}^(2) {(x - 2)}^(3) }{ {( {x}^(2) - 5x + 6) }^(2) \: (x + 5)} \geqslant 0 \\ \\ \end{gathered}`
Please answer! ​

Answer 1

x < -5 or x = 1 or 2 < x < 3 or x > 3

Explanation:

Given rational inequality:

`((x-1)^2(x-2)^3)/((x^2-5x+6)^2(x+5))\geq 0`

`\textsf{Factor }(x^2-5x+6):`

`\implies x^2-2x-3x+6`

`\implies x(x-2)-3(x-2)`

`\implies (x-3)(x-2)`

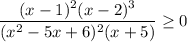
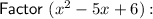
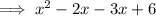
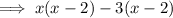
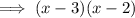
Therefore:

`((x-1)^2(x-2)^3)/((x-3)^2(x-2)^2(x+5))\geq 0`

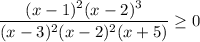
Find the roots by solving f(x) = 0 (set the numerator to zero):

`\implies (x-1)^2(x-2)^3=0`

`\implies (x-1)^2=0\implies x=1`

`\implies (x-2)^3=0 \implies x=2`

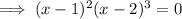
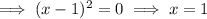
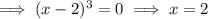
Find the restrictions by solving f(x) = undefined (set the denominator to zero):

`\implies (x-3)^2(x-2)^2(x+5)=0`

`\implies (x-3)^2=0 \implies x=3`

`\implies (x-2)^2=0 \implies x=2`

`\implies (x+5)=0 \implies x=-5`

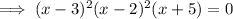
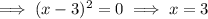
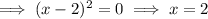
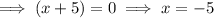
Create a sign chart, using closed dots for the roots and open dots for the restrictions (see attached).

Choose a test value for each region, including one to the left of all the critical values and one to the right of all the critical values.

Test values: -6, 0, 1.5, 2.5, 4

For each test value, determine if the function is positive or negative:

`f(-6)=((-6-1)^2(-6-2)^3)/((-6-3)^2(-6-2)^2(-6+5))=((+)(-))/((+)(+)(-))=+`

`f(0)=((0-1)^2(0-2)^3)/((0-3)^2(0-2)^2(0+5))=((+)(-))/((+)(+)(+))=-`

`f(1.5)=((1.5-1)^2(1.5-2)^3)/((1.5-3)^2(1.5-2)^2(1.5+5))=((+)(-))/((+)(+)(+))=-`

`f(2.5)=((2.5-1)^2(2.5-2)^3)/((2.5-3)^2(2.5-2)^2(2.5+5))=((+)(+))/((+)(+)(+))=+`

`f(4)=((4-1)^2(4-2)^3)/((4-3)^2(4-2)^2(4+5))=((+)(+))/((+)(+)(+))=+`

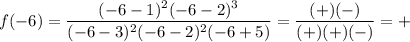
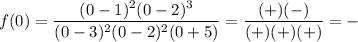
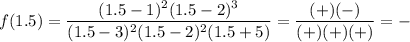
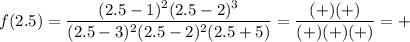
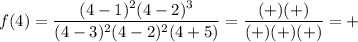
Record the results on the sign chart for each region (see attached).

As we need to find the values for which f(x) ≥ 0, shade the appropriate regions (zero or positive) on the sign chart (see attached).

Therefore, the solution set is:

x < -5 or x = 1 or 2 < x < 3 or x > 3

As interval notation:

`(- \infty,-5) \cup x=1 \cup (2,3) \cup(3,\infty)`