Answer:
See explanation
Explanation:
You are given the equation

1. Add 8 negative x-tiles to both sides of the equation to create a zero pair on the left side. The equation then will have form
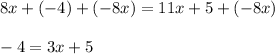
2. Add 5 negative unit tiles to both sides of the equation to create a zero pair on the right side. The equation now is
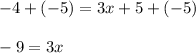
3. Divide both sides by 3:
