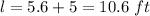Question

An oriental rug is 5 feet longer than it is wide. If the diagonal of the rug is 12 feet, find its dimensions to the nearest tenth of a foot.

Answer 1

`Width=5.6\ ft\\\\Lenght=10.6\ ft`

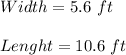
Explanation:

Let be:

"l" the lenght in feet of the oriental rug.

"w" the width in feet of the oriental rug.

"d" the length of the diagonal (in feet) of the oriental rug.

According to the exercise:

`l=w+5`

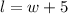
By definition, the diagonal of a rectangle can be calculated with the Pythagorean Theorem. Then, we can say that:

`d^2=l^2+w^2`

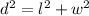
Now, we must substitute the equation
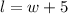`l=w+5` and the value of "d" into
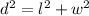`d^2=l^2+w^2` and then we must solve for "w":

`12^2=(w+5)^2+w^2\\\\144=w^2+2(w)(5)+5^2+w^2\\\\2w^2+10w-119=0`

Applying the Quadratic formula
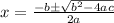`x=(-b\±√(b^2-4ac) )/(2a)`. we get:

`x=w=(-10\±√(10^2-4(2)(-119)))/(2(2))\\\\w_1=5.6\\\\w_2=-10.6`

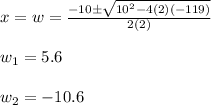
The width of the rug is the positive value:

`w=5.6\ ft`

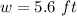
Finally, you can substitute the width into
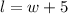`l=w+5` to find the length:

`l=5.6+5=10.6\ ft`