Question

Learning Goal: To introduce the idea of physical dimensions and to learn how to find them.Physical quantities are generally not purely numerical: They have a particular dimension or combination of dimensions associated with them. Thus, your height is not 74, but rather 74 inches, often expressed as 6 feet 2 inches. Although feet and inches are different units they have the same dimension--length. Find the dimensions [V] of volume. Find the dimensions [v] of speed.Express your answer as powers of length ( l), mass ( m), and time ( t)

Answer 1

volume : {l}^3

speed: (l)^1*(t)^-1

Step-by-step explanation:

Volume is a measure of 3 dimensional space. It is expressed with 3 orthogonal lengths. The volume of a box would be the product of it's height, width and length. These 3 are longitudes that can be expressed in meters, feet, inches, etc. Because these are 3 longitudes multiplied the result will be a cubic longitude (l)^3.

A more general method for finding a volume is to use integral calculus:

`V = \int\int\int{x} * {y} * {z} * dx * dy * dz`

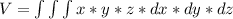
This is for Cartesian coordinates. Cylindrical and spherical coordinates can also be used.

Speed is defined as the rate of change in position respect of time:

`vx = (\delta x)/(\delta t)`

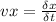
For movement in one dimension.

For movement in 3 dimensions you calculate the speed component of each space direction and express them as components of a speed vector:

`\v{v} = (\delta x)/(\delta t)  \hat{i} + (\delta y)/(\delta t)  \hat{j} + (\delta z)/(\delta t)  \hat{k}`

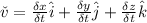
This is a vector of velocity components, each one is expressed as a division of a longitude over a time, so speed components have dimensions of (l)^1*(t)^-1

The speed vector has a magnitude that is obtained with the Pitagoras theorem:

`v = \sqrt{vx^(2) + vy^(2) + vz^(2)}`

Since each component is squared, added together and then the square root is taken this magnitude is also in (l)^1*(t)^-1