Answer:
The separation between slits is:
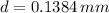
Step-by-step explanation:
The distance between adjacent maxima is given by the following expression:
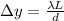
For the distance between maxima being 1mm (let's solve all this problem using milimeters) we have the following:
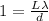 (1)
(1)
For the second condition in which the screen is moved 40 mm away we have the following:
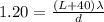 (2)
(2)
Using equation 1 we can write:
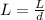
Plugging the value of L in equation 2 brings us to
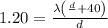
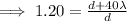
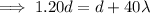
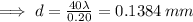
We could also as a bonus find L which is just
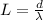
I'll leave that up to you! Good luck!